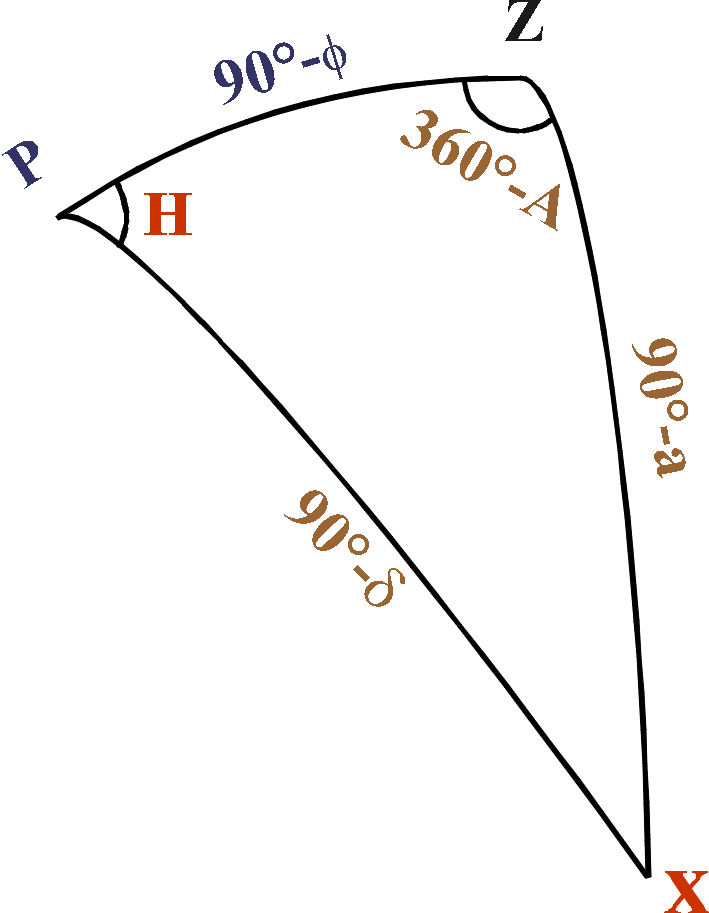
 Draw
"the" triangle again.
Draw
"the" triangle again.We require the azimuth A of point X,
where X is on the horizon (i.e. a=0)
and also on the equator (i.e. δ=0)
Exercise:
Prove that the celestial equator cuts the
horizon at azimuth 90° and 270°,
at any latitude (except at the North and South Poles).
 Draw
"the" triangle again.
Draw
"the" triangle again.
We require the azimuth A of point X,
where X is on the horizon (i.e. a=0)
and also on the equator (i.e. δ=0)
Apply the cosine rule:
cos PX = cos PZ cos XZ + sin PZ sin XZ cos Z
to get 0 = 0 + sin (90-φ) cos A
Since 90°-φ is not 0 (we are not at the Poles),
cos A must be 0
so A = 90° or 270° .
At what angle does the celestial equator cut the horizon, at latitude φ ?
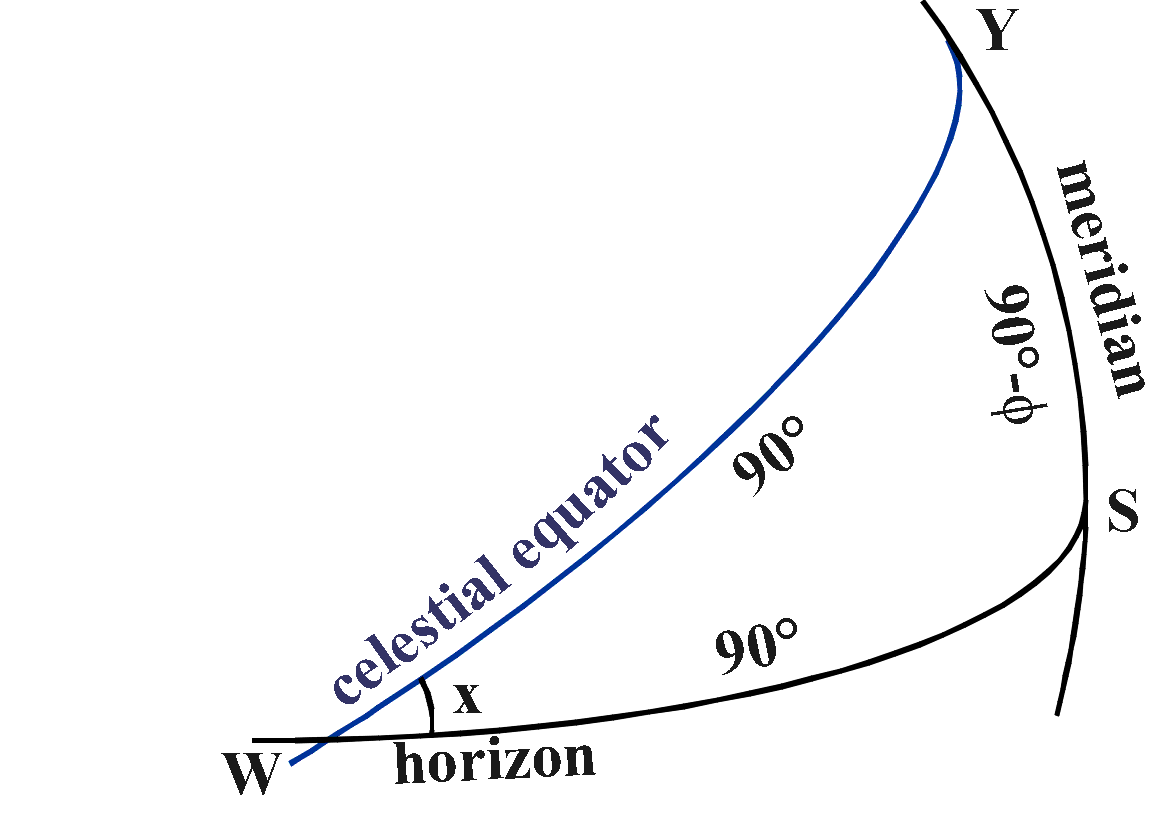 Use
the cosine formula:
Use
the cosine formula:
cos SY = cos SW cos YW + sin SW sin YW cos W
This gives cos (90°-φ) = 0 + cos x
So the angle x is 90°-φ.
The celestial equator cuts the horizon at an angle of 90°-φ
Back to "coordinate conversion".