Secondary Structures in Proteins

The reaction of an enzyme (E) with a substrate (S) to form a product (P) can be described as:

where ES is the enzyme-substrate complex (Michaelis complex).

Under steady-state conditions, the initial rate
of the reaction (v_o) is given by the Michaelis-
Menten equation:

The Lineweaver-Burk plot is a linear transformation of the Michaelis-Menten equation, and is useful for determining K_M and V_max graphically.
Compounds called inhibitors can interfere with the reaction. Inhibition can be competitive, uncompetitive, or of mixed type.

Competitive Inhibition

A competitive inhibitor, I, prevents the binding of substrate to the free enzyme, E, presumably by binding to the enzyme's active site. Thus, a competitive inhibitor competes directly with substrate for an enzyme's active site.

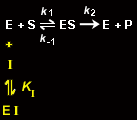
The inhibitor binds to the enzyme with the equilibrium constant K_I:

In competitve inhibition, the Michaelis-Menten equation takes the form:

where a = 1 + [I]/K_I. Hence, K_M(app) = aK_M, where K_M(app) is the apparent value of K_M. The Lineweaver-Burk equation then takes the form:

This describes a family of lines of slope aK_M/V_max that all intersect the 1/v_o axis at 1/V_max and have extrapolated intercepts on the 1/[S] axis of -1/aK_M.

Uncompetitive Inhibition

An uncompetitive inhibitor, I, binds to the enzyme-substrate complex ES but not to the free enzyme, E.
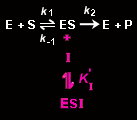
Equation 7a

Its binding prevents catalysis (ESI is catalytically inactive), presumably by altering the enzyme's active site. An uncompetitive inhibitor binds to the enzyme with the equilibrium constant K'_I:

In uncompetitive inhibition, the Michaelis-Menten equation takes the form:

where a' = 1 + [I]/K'_I. Hence, K_M(app) = K_M/a' and V_max(app) = V_max/a', where K_M(app) and V_max(app) are the apparent values of K_M and V_max.
The Lineweaver-Burk equation then takes the form:

This describes a family of parallel lines of slope K_M/V_max, whose intercepts on the 1/v_o axis are a'/V_max and whose extrapolated intercepts on the 1/[S] axis are -a'/ K_M.

Mixed Inhibition

A mixed inhibitor (alternatively, noncompetitive inhibitor), I, binds to both the enzyme, E, and to the enzyme-substrate complex, ES, thereby preventing the catalytic reaction.

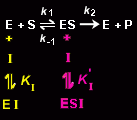
The inhibitor binds to the free enzyme with the equilibrium constant, K_I:

and to the enzyme-substrate complex with the equilibrium constant K'_I:

where K_I and K'_I are not necessarily equal.
In mixed inhibition, the Michaelis-Menten equation takes the form:

where a = 1 + [I]/K_I and a' = 1 + [I]/K'_I. Hence
K_M(app) = aK_M/a' and V_max(app) = V_max/a', where K_M(app) and V_max(app) are the apparent values of K_M and V_max.
The Lineweaver-Burk equation then takes the form:

This describes a family of lines that intersect to the left of the 1/v_o axis (on the 1/[S] axis in the special case that a = a'), whose intercepts on the 1/v_o axis are a'/V_max and whose extrapolated intercepts on the 1/[S] axis are -a'K_M/a.