CSCI 4312 Ch.
6 Exercises:
1. In CSMA/CD, after the 5th collision, what is the probability that a node chooses 𝐾 = 4?
2. (cont.) The result 𝐾 = 4 corresponds to a delay of how many seconds on a 10 Mbps Ethernet?
Hint: after mth collision, NIC chooses K at random from {0,1,2, , 2m-1}. NIC waits K*512 bit times, before attempting to send the frame again.
NOTE: 512 bit times = the amount of time needed to send 512 bits into the Ethernet
3. Why would the token-ring protocol be inefficient if a LAN had a very large perimeter?
4. How big is the MAC address space? The IPv4 address space? The IPv6 address space?
5. Subnetting
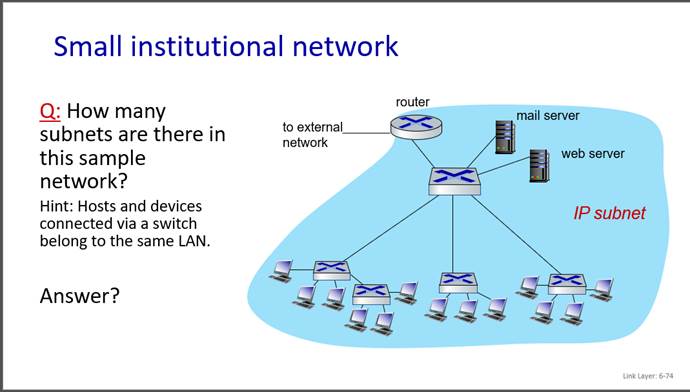
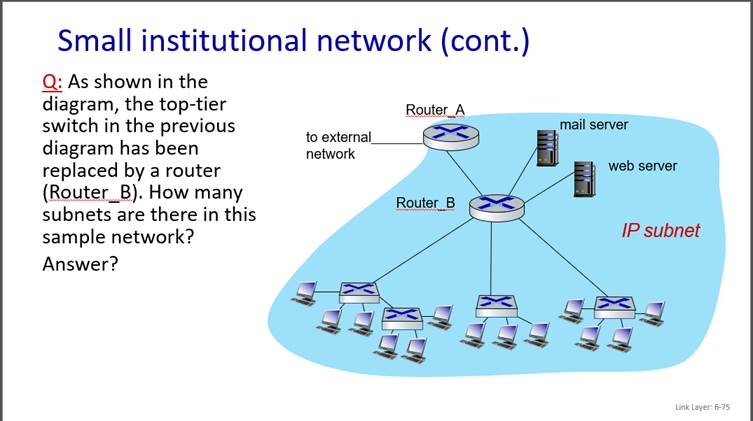
6. Subnetting (cont.)
7. Suppose nodes A, B, and C each attach to the same broadcast LAN (through their adapters). If A sends thousands of IP datagrams to B with each encapsulating frame addressed to the MAC address of B, will Cs adapter process these frames? If so, will Cs adapter pass the IP datagrams in these frames to the network layer C? How would your answers change if A sends frames with the MAC broadcast address?
8. Why is an ARP query sent within a broadcast frame? Why is an ARP response sent within a frame with a specific destination MAC address?
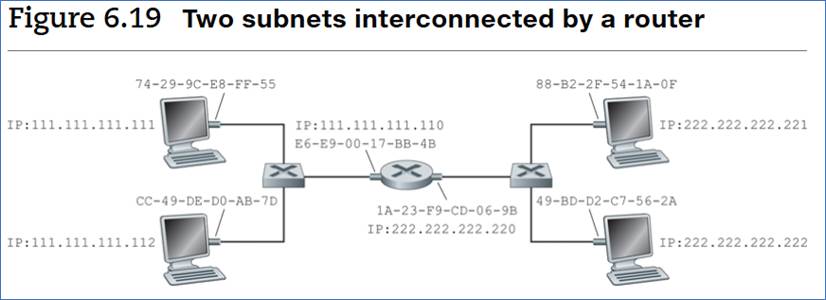
9. For the network in Figure 6.19, the router has two ARP modules, each with its own ARP table. Is it possible that the same MAC address appears in both tables?
10. Suppose a source data item contains 6 bytes: B7-0A-83-4F-E9-5C (as hexadecimal numbers). Show how the Internet checksum would be calculated for the data.
11. Galois Field, GF(2), calculation:
NOTE: All GF(2)
calculations are done in modulo-2 arithmetic without carries in addition or
borrows in subtraction. Addition and subtraction are identical, and both are
equivalent to the bitwise exclusive-or (XOR) of the operands.
Hint: To verify the result, use the calculator at http://www.ee.unb.ca/cgi-bin/tervo/calc.pl?num=10011111000&den=1001&f=d&e=1&m=1
a. 101011 1111
b. 101011 + 1111
c. 101011 / 1111
d. 101011 x 1111
12.
Cyclic Redundancy Check: Consider the 5-bit
generator, G = 10011, and suppose that D has the value 1010101010. What is the
value of R? Hint: The length of R (r) is the length of G minus 1.
13. (cont.) Show how the D and R would be validated by the receiver.