Redox Reactions
 
 
 
SECTIONS
  
     

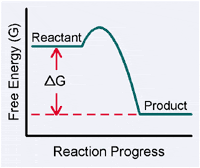
GIBBS FREE ENERGY OF REDOX REACTIONS

In the preceeding section, we learned that DE°' is the change in the reduction potential of a redox reaction. We also were shown that a positive DE°' value indicates a spontaneous reaction.

Changes in reduction potential are linked to changes in the free energy of a system

The field of thermodynamics is concerned with the flow of energy during chemical reactions. You should be familiar with the basic concepts of thermodynamics from general chemistry, but if you need to refresh your knowledge please visit the Thermodynamics Review. One of the core concepts of thermodynamics is that for any spontaneous reaction, free energy is lost. Spontaneous reactions always proceed “downhill” to create products containing less free energy than the reactants. This idea is expressed with a quantity called the Gibbs Free Energy change or DG°'.

Energy diagram: The free energy profile of a reaction going from products to reactants.

The Gibbs Free Energy change (DG°') is the quantity of usable energy (chemical potential) in a reaction. Here, DG°' is the difference between the free energy of the reaction products and the reactants:

DG°' = (energy of products) – (energy of reactants)

Since naturally occurring or “spontaneous” processes always proceed toward the state that has the least potential energy, the energy of the products is less than the energy of the reactants.

For a spontaneous process, DG°' is negative.

It is not surprising then that changes in the quantities of Gibbs Free Energy and reduction potential, DE°' and DG°', are related to one another, for both can be used to predict whether processes are spontaneous. Indeed, the relationship between these two quantities is given by the following formula:

DG°' = – nF(DE°')
where

DG°' is the Gibbs free energy change of a system (in Joules)
DE°' is the change in reduction potential of the redox reaction (in Volts)
n is the number of electrons transferred in the reaction (in moles)
F is Faraday’s constant (96,500 Joules/Volt/mol)

Notice that the relationship between DG°' and DE°' is an inverse one: when DE°' is positive, DG°' is negative, and vice versa. This makes sense because for spontaneous redox processes DG°' is negative and DE°' is negative.

Example 5

Determine the DG°' of the reaction:

malate + NAD+    oxaloacetate + NADH + H+

The two half reactions from the half reaction table are:

(1) oxaloacetate + 2 H+ + 2 e–    malate

E°' = –0.175 V
(2) NAD+ + 2H+ + 2 e–    NADH + H+

E°' = –0.320 V

First, we need to find the DE°' of the reaction:

The overall reaction consists of half reaction (2) added to the reverse of half reaction (1):

malate + NAD+ + 2H+ + 2e–    oxaloacetate + NADH + H+ + 2H+ + 2e–

Looking at the overall reaction, we can see that half reaction (2) functions as the reduction reaction (NAD+ gains electrons), and half reaction (1) functions as the oxidation reaction (malate loses electrons). The DE°' for the reaction is therefore

DE°' = (E°' from reduction reaction) – (E°' from oxidation reaction)
DE°' = (–0.320 V) – ( –0.175 V)
DE°' = –0.145 V

Then, use the formula to calculate DG°' :

DG°' = –nF(DE°')
DG°' = –(2 mol)(96,500 J/V/mol)(–0.145 V)
DG°' = 27,985 J
DG°' = 28 kJ