Acids, Bases, and pH
 
 
 
SECTIONS
  
     

THE HENDERSON–HASSELBALCH EQUATION

We have learned that the pH of a solution depends on the concentration of H+ (more correctly called H3O+) ions present in the solution. We have also learned that weak acids don’t fully dissociate into ions when placed in water. How much they ionize, or how “acid” they can make the water in which they dissolve, is different for each weak acid. The pKa is a measure of the weak acid’s ability to ionize. Thus, pH and pKa seem like very similar terms, and it is important not to get them confused. Remember, pH is a direct measure of the H+ concentration, while pKa represents a particular acid’s ability to ionize (dissociate into ions, including H+).

The Henderson–Hasselbalch equation

However, since the extent of ionization of a weak acid (the pKa) influences the final concentration of H+ ions (the pH) of the solution, there must be a relationship between pH and the pKa of a weak acid. This relationship is given by the Henderson–Hasselbalch equation:

pH

   =   pKa   +   log  [base]

[acid]

Where “base” represents the conjugate base, and “acid” the conjugate acid, of a conjugate acid–base pair (for a review of conjugate acid–base pairs see section 5). Note that there is a way for the pH and the pKa of a solution to be the same: the term “log [base]/[acid]” must be equal to zero! When does that happen? If we solve the equation

log [base]/[acid] = 0
[base]/[acid] = 1
[base] = [acid]

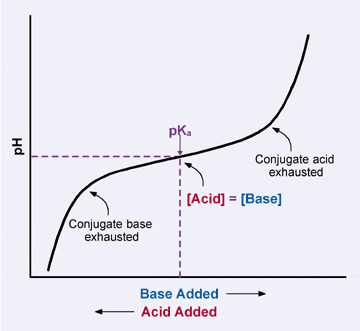
Thus, only in the rare circumstance when the molar concentrations of the conjugate acid and conjugate base in a solution are equal, the pH = pKa. Below is a graph of a weak acid titration, which is also a graph of the Henderson-Hasselbalch equation, showing how pH changes as acid or base is added. Note that when the pH = pKa, there are equivalent amounts of the conjugate acid and base. It is also important to note that just because the amounts of conjugate acid and base are the same at the pKa, the pH is not 7 (neutral) at this point. Remember, pH is a function of the the concentration of H3O+, not the conjugate acid, and because weak acids do not ionize completely, these concentrations will not be the same.

Buffer titration/Henderson–Hasselbalch graph: how the pH of a buffered solution changes as acid or base is added.

It is important to remember that the pH of a weak acid solution can be calculated, using the Ka value of the weak acid.

Example 4

What is the pH when 10 mL of 1 M acetic acid is added to pure water so that the final volume is 100 mL? The Ka for acetic acid is 1.74 x 10–5.

The reaction that occurs when acetic acid dissociates in water is

CH3COOH + H2O CH3COO– + H3O+

It is given that 10 mL of 1 M acetic acid is diluted to 100 mL in water. Thus, the initial acetic acid concentration is

(0.01 liter)(1 mol/liter) / (0.100 liter total volume) = 0.1 M acetic acid.

Once the acetic acid is diluted in water, the dissociation reaction begins and continues until it reaches equilibrium. We can use a table to organize what happens to all the species involved in the reaction:

ACETIC ACID DISSOCIATION TABLE
  CH3COOH CH3COO– H3O+
Initial concentration 0.1 M 0 0
Equilibrium concentration 0.1 M – [CH3COOH] [CH3COO–] [H3O+]

We also know that the Ka of acetic acid is 1.74 x 10–5 . Using the Ka expression for acetic acid:

Ka   =   [CH3COO–][ H3O+]
[CH3COOH]

Plugging in the known Ka value, as well as the equilibrium concentrations of each species:

1.74 x 10–5    =    [CH3COO–][ H3O+]
0.1 – [CH3COO–]

But since one H3O+ is produced for every CH3COO– ion,

[CH3COO–] = [ H3O+]

and the expression becomes

1.74 x 10–5   =   [ H3O+][ H3O+]
0.1 – [ H3O+]

This is of course now just an algebra problem, where we have an quadratic equation in the form of

1.74 x 10–5   =   x2
0.1 – x2

But don’t drag out that quadratic formula just yet! Thankfully there is a shortcut that we can use. Remember that weak acids dissociate very poorly in water, which means that the final CH3COO– concentration will be very small compared to the 0.1 M acetic acid that we started with. This means that the equilibrium concentration of CH3COOH will be very close to 0.1 M. This changes the Ka expression to

1.74 x 10–5    =    [CH3COO–][H3O+]
0.1

or

1.74 x 10–5    =    [H3O+][H3O+]
0.1

1.74 x 10–6 = [H3O+]2
[H3O+] = 1.32 x 10–3

Using the pH equation:

pH = – log [H3O+]
pH = – log (1.32 x 10–3)
pH = 2.88